Quantum Bit (Qubit)

Part of Womanium Quantum + AI 2024 program

Definition

A quantum bit (qubit), is a device that can be in one of two states, commonly represented by 0 and 1, however, this device doesn't act classically, it acts in a quantum manner, which will allow us to implement quantum computers.

Representation

To describe an isolated quantum system, we give and amplitude, $α$ , for each state that the system can be in when measured.

Alpha is a complex number, that means it's composed of a real and an imaginary part. $α = a + i b$

If a classical system of a single bit can be represented as

| \hat{v} ⟩ = p (\begin{matrix} 1 \\ 0 \end{matrix}) + (1 - p) (\begin{matrix} 0 \\ 1 \end{matrix})

Where $| ⟩$ is the bra-ket (Dirac) notation that describe the state of a system in a column vector.

Then a quantum system of a single qubit can be represented as

| ψ ⟩ = α (\begin{matrix} 1 \\ 0 \end{matrix}) + β (\begin{matrix} 0 \\ 1 \end{matrix})

However, it must be understood that the representation of quantum system is not a probability vector, but rather an amplitude vector, this means that $p_{0} \neq α$ .

Born Rule

The probability of measuring a quantum system in a state is the square of the absolute value of the state's amplitude.

Example: Probability of a qubit

| ψ ⟩

being in state 0.

$| ψ ⟩ = α (\begin{matrix} 1 \\ 0 \end{matrix}) + β (\begin{matrix} 0 \\ 1 \end{matrix})$

p_{0} = | α |^{2}

This implies that a valid qubit must satisfy $| α |^{2} + | β |^{2} = 1$ .

Notation

Ket Notation: Column vector

$| 0 ⟩ = (\begin{matrix} 1 \\ 0 \end{matrix})$
$| 1 ⟩ = (\begin{matrix} 0 \\ 1 \end{matrix})$

Bra Notation: Row vector

$⟨ 0 | = (\begin{matrix} 1 & 0 \end{matrix})$
$⟨ 1 | = (\begin{matrix} 0 & 1 \end{matrix})$

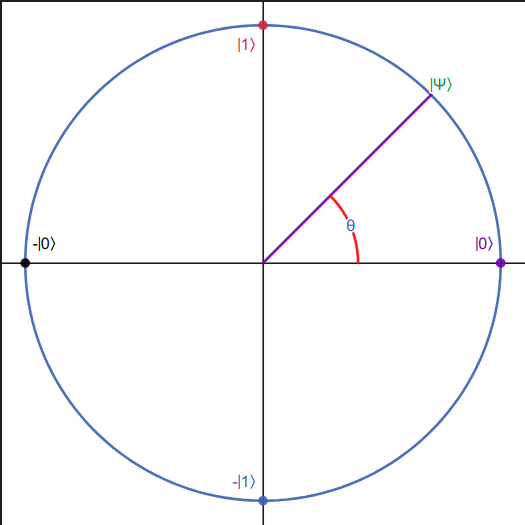
Real-Numbered Qubits

We can restrict a qubit amplitudes to real numbers, however if we restrict our system to real numbers we won't be able to picture all quantum operations but a subset of them. An example of an operation that requires complex numbers is Fourier Transformation which is used in Shor's prime factorization Algorithm.

If restricted to real numbers then we can represent a qubit amplitudes $α$ and $β$ as $c o s θ$ and $s i n θ$ .

| ψ ⟩ = (\begin{matrix} \cos θ \\ \sin θ \end{matrix})

Therefore we can visually represent a real-numbered qubit as a unit vector or a point on the unit circle

Pasted image 20240702170246.png

Summary

For a quantum system with n qubits, the quantum system state can be represented as

| ψ ⟩ = \sum_{i = 0}^{n^{2} - 1} α_{i} | i ⟩, \sum_{i = 0}^{n^{2} - 1} α_{i}^{2} = 1, α_{i} \in R

The probability to observe a particular output $i$ on measuring $| ψ ⟩$ is given by $α_{i}^{2}$ .

< Prev | Next: Quantum Operations >