Quantum Protocols

Part of Womanium Quantum + AI 2024 program

Definition

Quantum protocols are procedures that exploit quantum mechanics to achieve certain tasks. These protocols are not useful by themselves, but rather they are used as a building block for other algorithms.

Bell State Preparation

A bell state is a class of entangled qubits such that the quantum state, that a quantum system is in, can not be decomposed to a tensor product of multiple amplitude vectors.

This protocol focuses on creating entanglement between two qubits. Bell state preparation creates maximally entangled qubits, meaning that the qubits are perfectly correlated in their measurements.

To entangle the qubits we first make sure that the control bit is in a superposition, otherwise the result will be determined and won't make use of quantum mechanics, then we use an entanglement gate, the CNot gate is a popular entanglement gate.

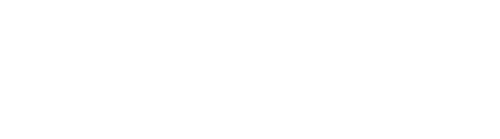
We notice that the output of this circuit will result in two perfectly correlated qubits, in other words two maximally entangled qubits.

Let's calculate the output step by step.

\begin{aligned} | 00 ⟩ & \overset{H \otimes I}{\to} | + 0 ⟩ = \frac{1}{\sqrt{2}} (| 00 ⟩ + | 10 ⟩) \\ \overset{I \otimes CNOT}{\to} \frac{1}{\sqrt{2}} (| 00 ⟩ + | 11 ⟩) = \frac{1}{\sqrt{2}} (\begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \end{array}) = | Φ^{+} ⟩ \end{aligned}

Here we can see that the result vector can not be decomposed to the tensor product of two vectors.

Superdense Coding

Is a protocol where 2 entangled qubits are needed to then encode 2 classical bits into one of the qubits, then decoding it back to 2 classical bits.

This protocol starts by preparing a bell state as can be seen in the figure, then applying 2 gates on the first qubit, the decoding it back to classical with the use of the second entangled qubit.

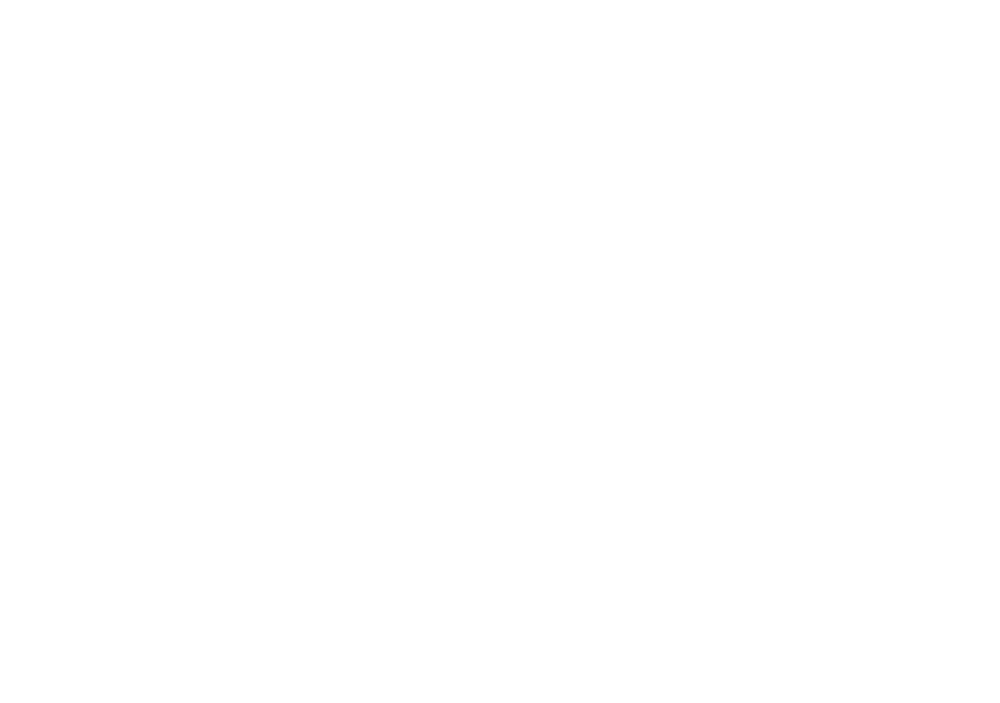
The quantum state of the system after each gate will be as follows, starting after the bell state $| Φ^{+} ⟩$

$b_{1}, b_{2}$	$C N O T \otimes I$	$C Z \otimes I$	$I \otimes C N O T$	$H \otimes I$
$0, 0$	$\| Φ^{+} ⟩$	$\| Φ^{+} ⟩$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ + \| 10 ⟩) = \| + ⟩ \| 0 ⟩$	$\| 00 ⟩$
$0, 1$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 11 ⟩ + \| 01 ⟩) = \| + ⟩ \| 1 ⟩$	$\| 01 ⟩$
$1, 0$	$\| Φ^{+} ⟩$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ - \| 11 ⟩)$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ - \| 10 ⟩) = \| - ⟩ \| 0 ⟩$	$\| 10 ⟩$
$1, 1$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 01 ⟩ - \| 10 ⟩)$	$\frac{1}{\sqrt{2}} (\| 01 ⟩ - \| 11 ⟩) = \| - ⟩ \| 1 ⟩$	$\| 11 ⟩$

We can see that the result of this circuit matches the 2 classical bits that we started with, by only doing operations on the first qubit without directly sending the classical bits.

Quantum Teleportation

Quantum teleportation is the process of copying the quantum state of one qubit to another, the quantum state can be stored in 2 classical bits to then reconstruct a qubit with the first qubit's state. However, this operation doesn't defy the no-cloning theorem, such that the first qubit state must be collapsed for it to be copied, also it requires the use of entanglement between 2 other qubits.

Again, as we can see in the figure, this protocol relies of having a bell state at the start between two qubits.

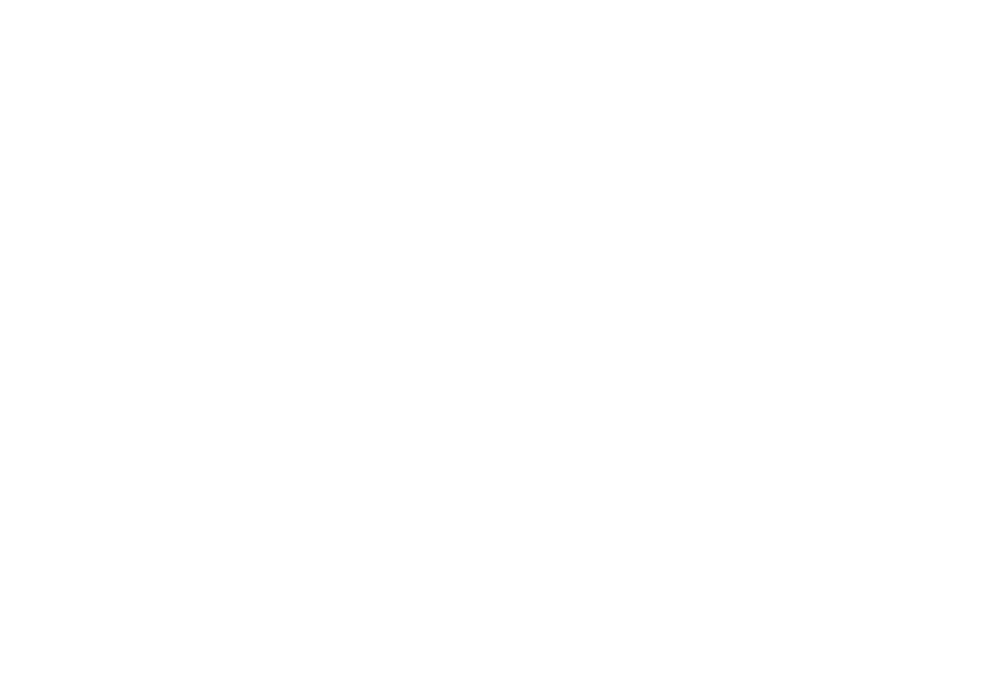
The state of the system after each gate will be as follows, starting after the bell state $| Φ^{+} ⟩$ , so we start with $| ψ ⟩ | Φ^{+} ⟩$

\begin{aligned} | ψ ⟩ \otimes | Φ^{+} ⟩ & = (α | 0 ⟩ + β | 1 ⟩) \frac{1}{\sqrt{2}} (| 00 ⟩ + | 11 ⟩) \\ = \frac{1}{\sqrt{2}} (α | 000 ⟩ + α | 011 ⟩ + β | 100 ⟩ + β | 111 ⟩) \\ \overset{I \otimes CNOT \otimes I}{\to} & \frac{1}{\sqrt{2}} (α | 000 ⟩ + α | 011 ⟩ + β | 110 ⟩ + β | 101 ⟩) \\ \overset{H \otimes I \otimes I}{\to} & \frac{1}{2} (α | 000 ⟩ + α | 100 ⟩ + α | 011 ⟩ + α | 111 ⟩ + β | 010 ⟩ - β | 110 ⟩ + β | 001 ⟩ - β | 101 ⟩) \\ = \frac{1}{2} (| 00 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 01 ⟩ (α | 1 ⟩ + β | 0 ⟩) + | 10 ⟩ (α | 0 ⟩ - β | 1 ⟩) + | 11 ⟩ (α | 1 ⟩ - β | 0 ⟩)) \\ \overset{I \otimes I \otimes C N O T}{\to} & \frac{1}{2} (| 00 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 01 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 10 ⟩ (α | 0 ⟩ - β | 1 ⟩) + | 11 ⟩ (α | 0 ⟩ - β | 1 ⟩)) \\ \overset{I \otimes I \otimes C Z}{\to} & \frac{1}{2} (| 00 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 01 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 10 ⟩ (α | 0 ⟩ + β | 1 ⟩) + | 11 ⟩ (α | 0 ⟩ + β | 1 ⟩)) \\ = \frac{1}{2} ((| 00 ⟩ + | 01 ⟩ + | 10 ⟩ + | 11 ⟩) (α | 0 ⟩ + β | 1 ⟩)) \\ = \frac{1}{2} (| 0 ⟩ + | 1 ⟩) (| 0 ⟩ + | 1 ⟩) | ϕ ⟩ \\ = | + ⟩ | + ⟩ | ϕ ⟩ \end{aligned}

Phew. That's a lot of math.

Although the first and second qubits collapsed after the measurement, I kept them in the calculation to illustrate their control in the CNOT and CZ gates.

We can see that the quantum state of the first qubit was "teleported" to the last qubit.

< Prev | Next: Phase Kickback >

$b_{1}, b_{2}$	$C N O T \otimes I$	$C Z \otimes I$	$I \otimes C N O T$	$H \otimes I$
$0, 0$	$\| Φ^{+} ⟩$	$\| Φ^{+} ⟩$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ + \| 10 ⟩) = \| + ⟩ \| 0 ⟩$	$\| 00 ⟩$
$0, 1$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 11 ⟩ + \| 01 ⟩) = \| + ⟩ \| 1 ⟩$	$\| 01 ⟩$
$1, 0$	$\| Φ^{+} ⟩$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ - \| 11 ⟩)$	$\frac{1}{\sqrt{2}} (\| 00 ⟩ - \| 10 ⟩) = \| - ⟩ \| 0 ⟩$	$\| 10 ⟩$
$1, 1$	$\frac{1}{\sqrt{2}} (\| 10 ⟩ + \| 01 ⟩)$	$\frac{1}{\sqrt{2}} (\| 01 ⟩ - \| 10 ⟩)$	$\frac{1}{\sqrt{2}} (\| 01 ⟩ - \| 11 ⟩) = \| - ⟩ \| 1 ⟩$	$\| 11 ⟩$