Combinatorial Optimization
Part of Womanium Quantum + AI 2024 program
Definition
Combinatorial optimization is a field focused on finding the optimal solution for a problem from a finite set of possible solution. This is mainly achieved by minimizing or maximizing a function by selecting the optimal combination of elements according to the problem and its constraints.
In many of combinatorial optimization problems a complete search is practical for real-world applications, since the search space of all possible solutions gets too big for a brute-force approach to be effective.
Examples of Combinatorial Optimization Problems
Traveling Salesman Problem (TSP)
Travelling salesman problem (TSP) is one of the most famous problems in computer science, the problem is defined on a graph such that each vertex represents a city and the edges represent roads between these cities. The goal is to find the shortest path that visits every city exactly once. The problem doesn't define a starting nor an ending city, therefore these can be arbitrary.
A path through a graph that visits each vertex exactly once is called a hamiltonian path or a hamiltonian cycle if it is a closed path.
As of any other optimization problem, the simplest approach to solve the problem is brute-force, however, the time needed to solve the problem for a given graph increases rapidly when the graph gets bigger.
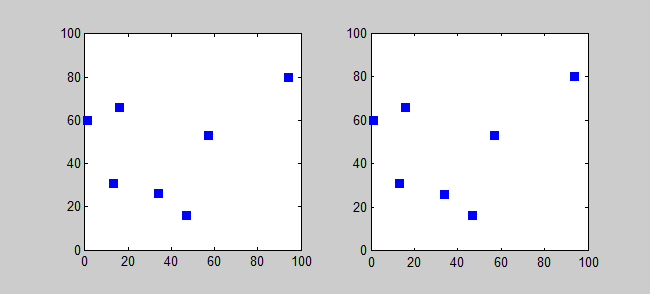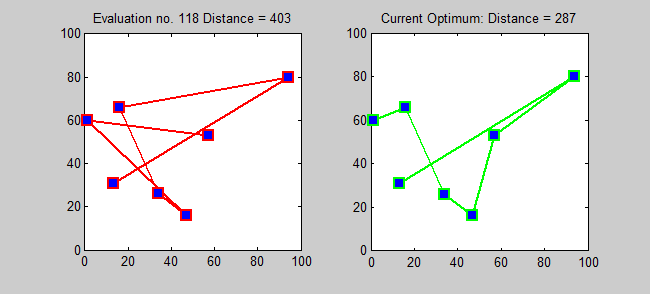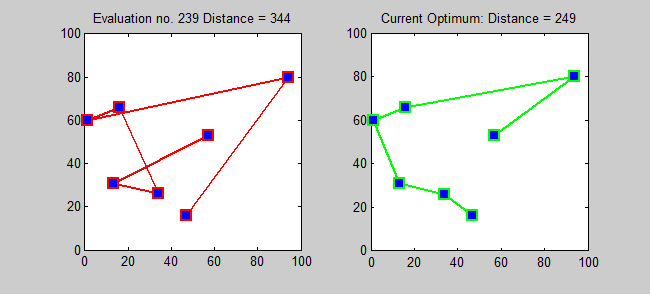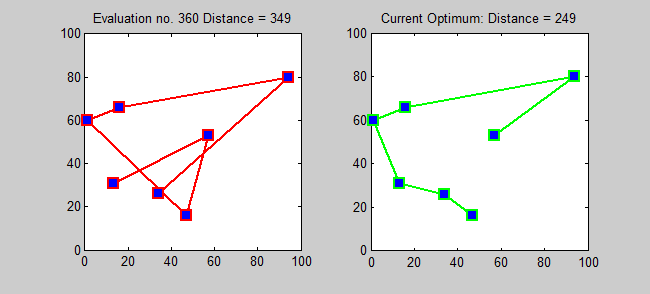
The following shows a program solving the travelling salesman problem using brute-force. (source: Wikipedia)
Graph Coloring Problem
Graph coloring is another graph problem where each vertex is colored such that no two adjacent vertices have the same color. The goal is to find the smallest number of colors required to achieve that constraint.
The smallest number of colors required to color a graph is called the chromatic number.
One approach to solve the graph coloring problem is the greedy approach, which results in an approximate solution and not an optimal solution. The idea is to check multiple numbers of colors until the smallest viable solution is found.
The algorithm starts at an arbitrary vertex and give it the first color, then it moves to its neighboring vertices and assigns them the next color, and so on until the entire graph is traversed without having neighboring vertices with the same color.
Max-Cut Problem
The max-cut problem is another graph problem, where the goal is to split the vertices into two disjoint sets such that the number of edges connecting the two sets is maximum.
The simplest case of solving the max-cut problem is when the graph is bipartite, which means the graph vertices can be divided into two disjoint sets such that all edges connect the two sets.
We've seen before how we can solve the max-cut problem can be solved using Grover's Search and went into more details in a previous page in QNickel.