Max-Cut Problem

#quantum #qnickel

Part of Womanium Quantum + AI 2024 program

Definition

The max-cut problem is a problem defined on a graph. Its primary goal is to divide the vertices of the graph into to disjoint sets such that the number of edges connecting the two sets is maximized.

Another way to describe the problem is by separating the vertices in the two disjoint sets using two colors, usually blue and red. We then count the number of edges that connect a blue vertex with a red one.

There are $2^n$ possible pairs of disjoint sets that we must search through to find the maximum cut. This makes the max-cut problem computationally challenging, and it is classified as NP-Complete.

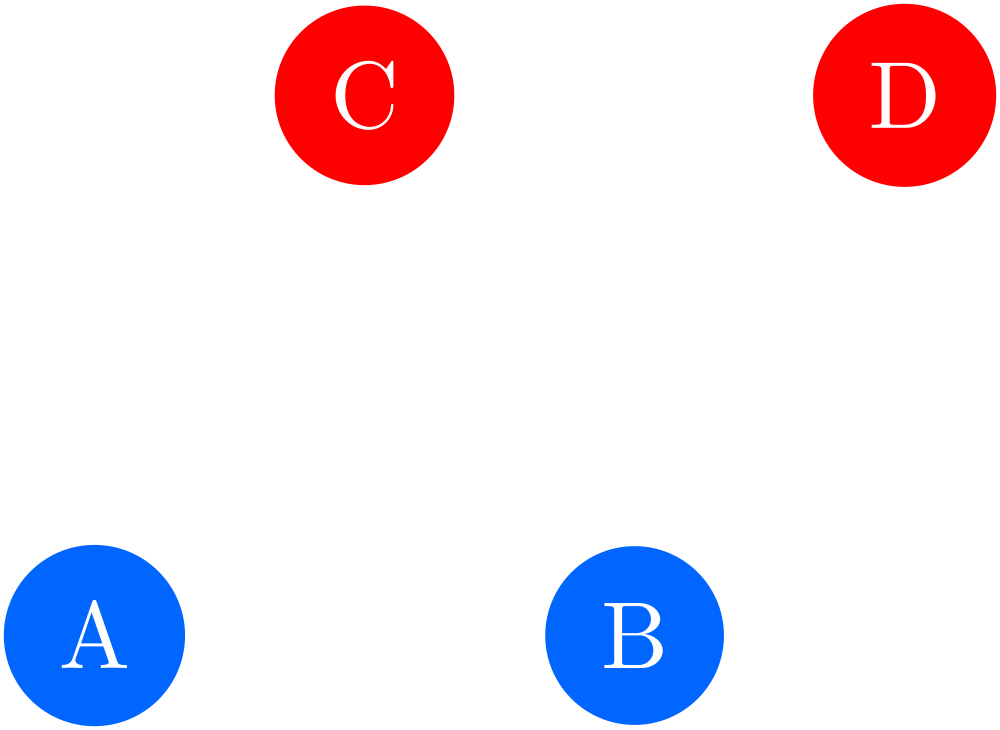
Bipartite Graphs

A bipartite graph is a graph that can be split into two disjoint sets such that all edges connect vertices between the two sets. In other words, no edge connect two vertices in the same set.

This can be defined mathematically as a graph $G=(V,E)$ where the set of vertices $V$ can be divided to two disjoint sets $U$ and $W$ such that $V=U\cup W$ and $U\cap W=\mathrm{\varnothing }$. Each edge $e\in E$ connects vertices from different sets, $E\subseteq (u,w)|u\in U,w\in W$.

From the properties of bipartite graphs, we conclude that the max-cut of any bipartite graph is equal to the number of edges $|E|$ in the graph. Therefore, bipartite graphs are among the simplest types of graphs to find their max-cut.

We utilize this by first checking if a graph is bipartite before applying a general algorithm to compute the max-cut.

Checking Bipartiteness

We check if a graph is bipartite by finding a 2-coloring such that all edges connect vertices of different colors.

We start by assigning a qubit to each vertex of the graph, and we define the state $|0⟩$ to represent red, and state $|1⟩$ represents blue.

Then we need to check if an edge connect two vertices of different color, we achieve that using an XOR gate, which checks if only one of the vertices is in the $|1⟩$ state. The following image shows an implementation of the XOR gate.

Since we need to apply an XOR gate for each edge and store that value, we need additional qubits for each edge. Then we can check if all edges connect 2 different colors by using a CX gate controlled by all edge qubits and the target is an additional ancilla qubit.

Now we can wrap up all of this in an oracle that checks for bipartiteness.

The following pseudo code shows an implementation of the oracle.

def oracle_function(E, ancilla):
	# apply XOR gate on each edge with its vertices as input
	EQ = [] # list of all edge qubits
	for e, u, w in E:
		XOR(u, w, e)
		EQ.append(e)

	# apply MCX controlled by all edge qubits
	MCX(EQ, ancilla)

def oracle(E, ancilla):
	# apply function
	oracle_function(E, ancilla)
	
	# flip the phase of the correct state
	Z(ancilla)

	# reverse all operations done on additional qubits
	reverse(oracle_function(E, ancilla))

Using Grover's Search

After defining an oracle that can check for graph bipartiteness, now we can use Grover's search to find whether a graph is bipartite or not.

The following pseudo code shows how Grover's search can be implemented to check for bipartiteness.

def grover_diffusion(V):
	# apply the diffusion operator (2|h><h| - I)
	H(V)
	X(V)
	CZ(V[:-1], V[-1])
	X(V)
	H(V)

def grover_search(k, V, E, ancilla):
	# initalize all vertices states in superposition
	H(V)

	# apply grover's algorithm k times
	for i in range(k):
		oracle(E, ancilla)
		grover_diffusion(V)

Solving Max-Cut for Any Graph

After implementing an algorithm to check whether a graph is bipartite, we can generalize this implementation to solve the max-cut problem. In our previous implementation, the algorithm checked if all edge qubits are equal to one, meaning that the sum of all edge qubits equals the number of edges in the graph.

We can modify this check to ensure the sum is at least some value $k$. This allows us to determine if a graph cut exists such that the number of edges connecting the two sets is at least $k$. We implement this by counting the number of edge qubits in state $|1⟩$, then checking if the number is greater or equal to k.

The following pseudo code shows how to modify the oracle to check if the number of edges connecting the two sets is at least 4.

def oracle_function(E, ancilla):
	# apply XOR gate on each edge with its vertices as input
	for e, u, w in E:
		XOR(u, w, e)

	# calculate the summation of all edge qubits
	# stores result in the number qubits
	sum_qubits(E, number)

	# check if the summation >= k, if so apply X to ancilla 
	check_number(number, k, ancilla, oper=">=")

Conclusion

The max-cut problem is one practical application of quantum algorithms. In our proposed quantum solution, the complexity for checking if the number of edges connecting the two sets is greater or equal to k is $O(\sqrt{2^{|V|}})$, where $|V|$ is the number of vertices in the graph.

< Prev