Numbers and Adders

Part of Womanium Quantum + AI 2024 program

Introduction

Being able to represent numbers and manipulate them is a crucial part of computers. In classical computers we represent numbers in binary and we use gates such as half-adders and a full-adders to perform mathematical operations on them.

In quantum computers, we will also represent a number in binary, but we need to find a equivalent circuit for a half-adder.

Classical Adder

In classical computers we perform a half-adder on two bits and we output another two bits, summation result and a carry out. The following truth table shows the output of the half-adder for every possible permutation of the bits a and b.

a	b	sum	c_out
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

This gate is implemented using an XOR gate that takes in a and b and results in sum, and an AND gate that takes in a and b and results in c_out. The truth table of the XOR and AND gates proves the correctness of this implementation.

a	b	XOR	AND
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Quantum Adder

We already know that we can implement a quantum AND gate using a Controlled-X gate where the control qubits are the input and the target qubit is the output.

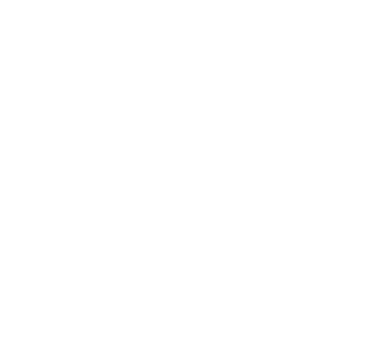
AND.png|250

Implementing a quantum XOR is similar and also uses Controlled-X gates, we first apply a CX from our first qubit to the output qubit then apply another CX from the second qubit to the target, this will flip the state of the target qubit if any of the input qubits are one, but if both are one then they will cancel each other.

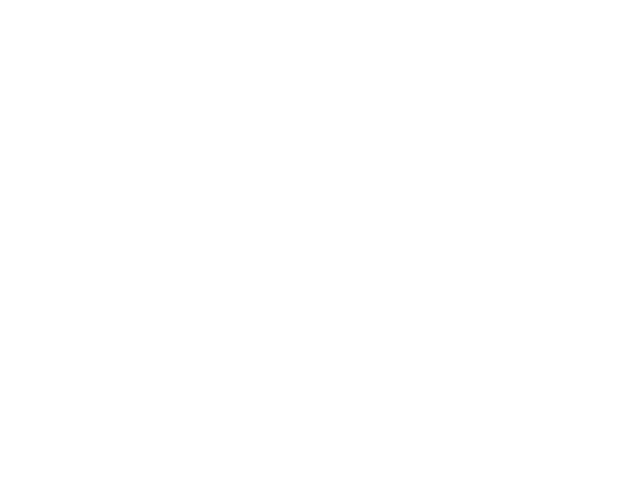
XOR.png|400
Now we can create a half-adder circuit just like we do classically but with the quantum implementation of the XOR and AND gates.

The following circuit shows the implementation of a half-adder, where qubits $q_{0}$ and $q_{1}$ are the inputs, $q_{2}$ represents the sum, and $q_{3}$ is the carry out.

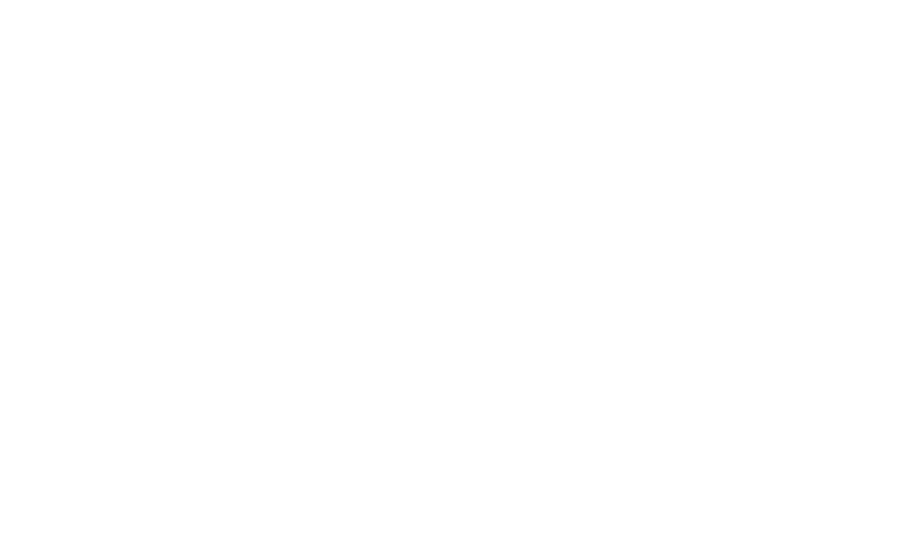
half-adder.png|500

In-Place Addition

We notice that the half-adder we constructed stores the result in a new qubit, but we may want to store the result in one of the input qubits instead of using another qubit. We implement that by applying a CX gate where the target is the qubit that will hold the result and controlled by the other input qubit.

We could also add another qubit to store the carry out of the summation. However, since we are applying and in-place operation, it's important to compute the carry out before the sum because the sum will override one of our qubits.

The following circuit shows the implementation of $q_{0} = q_{0} + q_{1}$ with $q_{2}$ being the carry qubit.

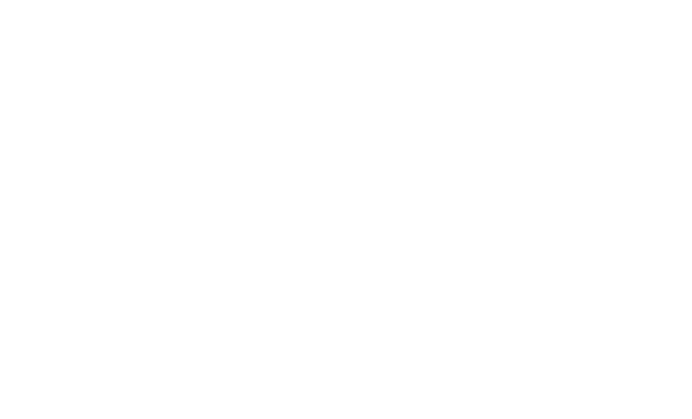
in-place addition.png|350

Counting

One important application of adders is counting the number of qubits that are in the $| 1 ⟩$ state, we do that by adding the qubits to an array of qubits such that it's size is at least $⌈ \log_{2} n ⌉$ , where $n$ is the number of summed qubits.

Note

We may also call this array a quantum number and its size is the number of qubits that it uses.

To count with multiple qubits, we treat the first qubit as the sum and the second as the carry out and the third as the carry out for the last qubit and so on.

Example:
Let's say that we have 3 qubits in the state $| ψ_{2} ⟩ | ψ_{1} ⟩ | ψ_{0} ⟩$ and we want to add them to a number of size 2 initialized at sate $| 000 ⟩$ . Let's define our input qubits as $q_{0}, q_{1}, q_{2}$ and out numbers qubits as $q_{3}, q_{4}, q_{5}$

We start by checking for an overflow to the last qubit, we do that by using CX gate controlled by the first 2 qubits of the number and the summed qubit, the following pseudo code shows this application

# Example: 1 + 011 -> 111
X(q5).controlled_by(q0, q3, q4)

Then we do the same for the qubit $q_{4}$ :

# Example: 1 + 01 -> 11
X(q4).controlled_by(q0, q3)

and finally we add the qubit to the first qubit:

# Example 1 + 1 -> 0
X(q3).controlled_by(q0)

We apply the same operations to the qubits $q_{1}$ and $q_{2}$ to finish the addition $q_{5} q_{4} q_{3} = q_{0} + q_{1} + q_{2}$ .

Note

For adding the first qubit to the number $| 000 ⟩$ we don't have to check for overflow, the first 2 operations can be omitted, but we note them to easily generalize the concept.

The following circuit shows the full implementation of this operation.

3bit addition.png|700

Number Checking

After we have a quantum number we will probably need to base other operations of the value of the number, checking and comparing the value of the number works just like working with any binary number, the difference is that we use CX gates to check the value.

Checking for Equality

To check if our quantum number is equal to some value $x$ we first need convert the value $x$ to binary then we check if the qubits of the quantum number are equal to the binary representation of $x$ .

Example:

Check if a quantum number of 3 qubits $(q_{0}, q_{1}, q_{2})$ is equal to the number 5 and store the condition result in flag qubit $q_{4}$ .

First we convert 5 to binary:

5_{10} = 101_{2}

Now we use a CX gate to check if our quantum number is equal to 101. But if we set the first and last qubits as the control and left out the second qubit then we would be checking if the number is equal to 5 or 7 since the second qubit can be either 0 or 1 without affecting the flag.

To solve that we flip all qubits that we expect to be in the zero state, using X gates, then we include them in the control of the CX gate, finally we apply X gates again to the same qubits to return them to their original values.

The following pseudo code show this operation.

X(q1) # flip 0 to 1
X(q4).controlled_by(q0, q1, q2)
X(q1) # return the flipped qubit to 0

And the following is the circuit implementation.

equality.png|400

Checking for Inequality

We apply a similar process as we did in the checking for equality but we don't include all qubits in controlling the CX gate to let them be either 0 or 1 such that they still satisfy the condition.

Example:
Check if the a quantum number of 3 qubits $(q_{0}, q_{1}, q_{2})$ is greater or equal to 4. Store the result of the condition in $q_{3}$ .

Convert 4 to binary.

4_{2} = 100_{2}

We notice that at least the most significant bit (MSB) has to be one, if any other bit is also 1 then the number will be greater than 4.

The following pseudo code checks for the MSB of the quantum number and therefore checking if $q_{2} q_{1} q_{0} \geq 4$ .

X(q3).controlled_by(q2)

Checking for

< n

To check if the number is less than a number n we can either use the operation as checking for $\geq$ then apply an X gate on the flag qubit, or we can check if that most significant bit that's equal to one in $n$ is equal to zero in the quantum number.

We can build on the same concepts to check for $>$ and $\leq$ .

< Prev | Next: Max-Cut Problem >